Thuật toán RSA và AES

Trong thời đại kỹ thuật số hiện nay, Internet là một công cụ hữu ích giúp người dùng giao tiếp và trao đổi thông tin với nhau một cách dễ dàng, nhanh chóng. Tuy nhiên vấn đề đặt ra là làm thế nào để bảo vệ những thiết bị truy cập mạng như điện thoại, máy tính. Hai thuật toán nổi bật trong bài toán bảo mật là RSA và AES. Mỗi thuật toán đều có những đặc điểm, ứng dụng và lợi ích riêng, phù hợp với các bối cảnh khác nhau.

1. Khái niệm

RSA

RSA (Rivest–Shamir–Adleman) là một hệ mã hoá bất đối xứng (asymmetric cryptography) sử dụng hai khoá khác nhau để mã hoá và giải mã.

Public key (khóa công khai) được chia sẻ với bất kỳ ai và dùng để mã hóa thông tin, trong khi private key (khóa bí mật) được giữ kín và chỉ người sở hữu nó mới có thể giải mã thông tin.

Bằng cách sử dụng public key, bất kỳ ai cũng có thể gửi thông tin một cách an toàn, nhưng chỉ người giữ private key mới có thể đọc được thông điệp. Điều này mang lại mức độ bảo mật cao vì dù thông tin có bị chặn, chỉ người có private key mới có thể giải mã.

AES

AES (Advanced Encryption Standard) là một thuật toán mã hóa đối xứng được sử dụng để bảo vệ dữ liệu trong các hệ thống máy tính và mạng.

Thuật toán AES sử dụng cùng một khóa cho việc mã hóa và giải mã dữ liệu, là một dạng mã hóa đối xứng. AES hoạt động trên các khối dữ liệu có kích thước cố định (128 bit) và có thể sử dụng các khóa với độ dài khác nhau (128, 192 hoặc 256 bit) để tăng cường tính bảo mật.

2. Nguyên lý hoạt động

RSA

Quá trình sinh khóa

Việc tạo khóa trong RSA dựa trên việc tìm ra bộ ba số tự nhiên: e, d, và n, với yêu cầu rằng khi mã hóa và giải mã thông điệp M, công thức sau được thỏa mãn:

m^e mod n = m^d mod n

Một điểm quan trọng là private key d phải được bảo mật tuyệt đối. Ngay cả khi ai đó biết được e, n, hay thông điệp m, họ cũng không thể tính được d. Cụ thể, quá trình sinh khóa trong RSA gồm các bước như sau:

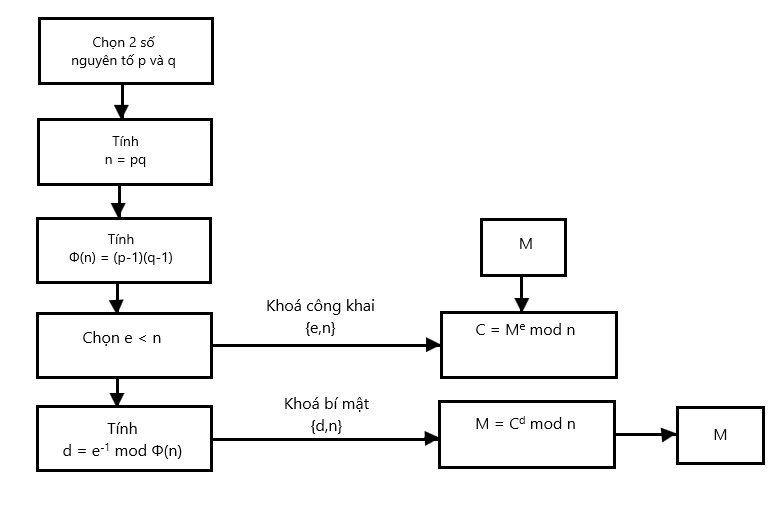
• Chọn hai số nguyên tố lớn p và q: Đây là hai số bí mật mà chỉ người tạo khóa mới biết.
• Tính giá trị n = p q: Giá trị này sẽ được dùng làm modulus cho cả public key và private key.
• Tính phi hàm Carmichael λ(n): Đây là một số giả nguyên tố được tính bằng cách lấy bội chung nhỏ nhất (BCNN) của λ(p) và λ(q), với λ(p) = p – 1 và λ(q) = q – 1. Giá trị λ(n) sẽ được giữ bí mật.
• Chọn số tự nhiên e: Chọn một số e trong khoảng (1, λ(n)) sao cho ƯCLN(e, λ(n)) = 1, nghĩa là e và λ(n) nguyên tố cùng nhau. Số e sẽ được dùng để mã hóa thông điệp.
• Tính số d: Tìm số d sao cho d e ≡ 1 mod λ(n), hay nói cách khác, d là nghịch đảo modulo của e theo λ(n). Số d này sẽ được dùng để giải mã thông điệp.
• Public key: Là bộ số (n, e), và có thể chia sẻ công khai.
• Private key: Là bộ số (n, d), cần được giữ bí mật.

Mã hoá và giải mã

Trong quá trình mã hóa và giải mã bằng RSA, chúng ta sử dụng public key (n, e) để mã hóa và private key (n, d) để giải mã. Dưới đây là các bước chi tiết:

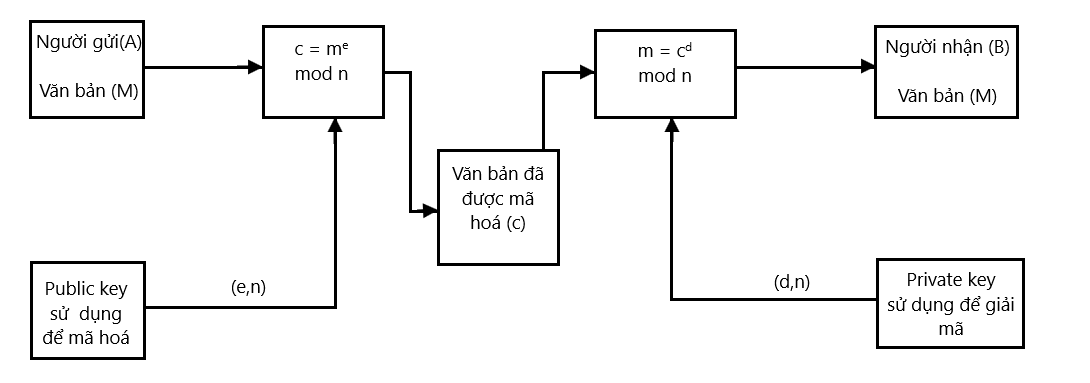
Mã hóa: Khi có một bản rõ (thông điệp) M, ta cần chuyển nó thành một số tự nhiên m sao cho 0 < m < n và m nguyên tố cùng nhau với n. Điều này có thể thực hiện dễ dàng bằng cách sử dụng các kỹ thuật padding (thêm dữ liệu bổ sung). Sau đó, ta tiến hành mã hóa số m thành c (bản mã) bằng công thức:

C = M^e mod n

Giá trị c sau đó sẽ được gửi tới người nhận.

Giải mã: Người nhận sử dụng private key (n, d) để giải mã bản mã c nhằm lấy lại số m bằng công thức:

M = C^d mod n

Sau khi có m, ta có thể khôi phục lại bản tin ban đầu M bằng cách đảo ngược quá trình padding.

AES

AES gồm ba mật mã khối AES-128, AES-192, AES-256 tương ứng với độ dài của key là 128 bit, 192 bit và 256 bit. Số vòng của key khác nhau, cụ thể 10 vòng cho 128 bit, 12 vòng cho 192 bit và 14 vòng cho 256 bit. Mỗi vòng đều thực hiện ba bước thay thế, biến đổi và hòa trộn khối plain text (văn bản thuần túy) đầu vào để biến nó thành Ciphertext (văn bản đã mã hóa).

Mỗi khối dữ liệu 128 bit đầu vào được chia thành 16 byte (mỗi byte 8 bit),có thể xếp thành 4 cột, mỗi cột 4 phần tử hay là một ma trận 4x4 của các byte, nó được gọi là ma trận trạng thái.

• Chuẩn bị dữ liệu: Dữ liệu cần được chia thành các khối 16 byte và được lưu trữ trong một ma trận 4x4 gọi là trạng thái. Nếu dữ liệu không đủ 16 byte, có thể sử dụng các kỹ thuật như đệm (padding) hay chuẩn hóa (normalization) để bổ sung.
• Chuẩn bị khóa: Khóa bí mật cũng cần được chia thành các khối 16 byte và được lưu trữ trong một ma trận 4x4 gọi là khóa vòng. Tùy vào độ dài của khóa ban đầu, có thể sinh ra từ 10 đến 14 khóa vòng khác nhau bằng cách sử dụng các phép biến đổi như hoán vị, thay thế và XOR.

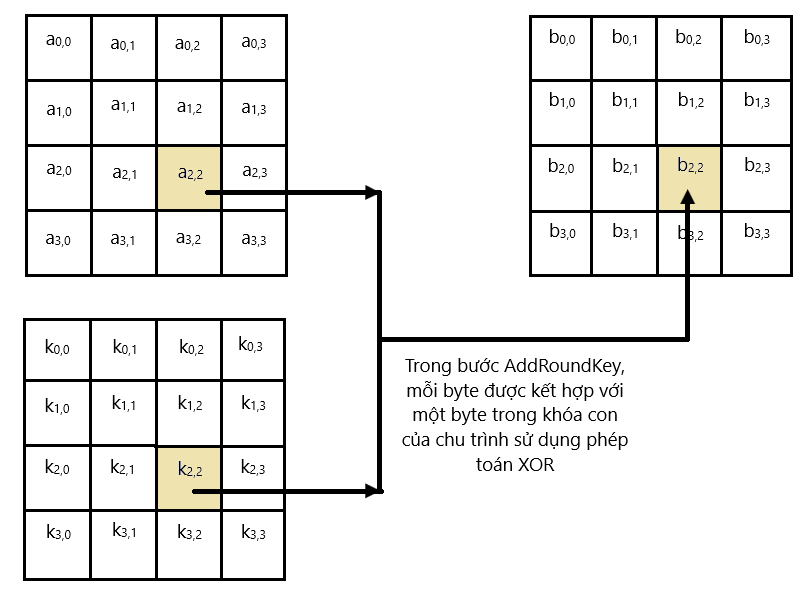
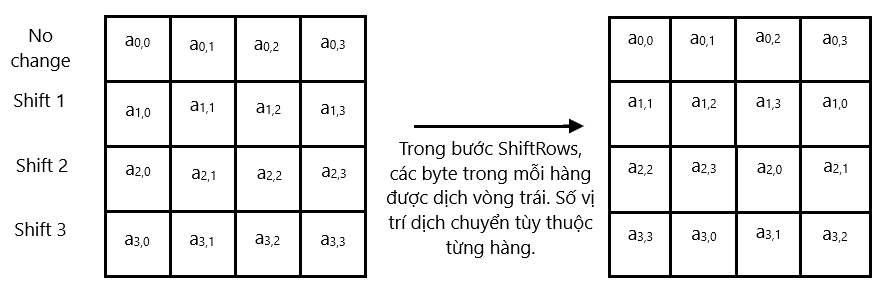
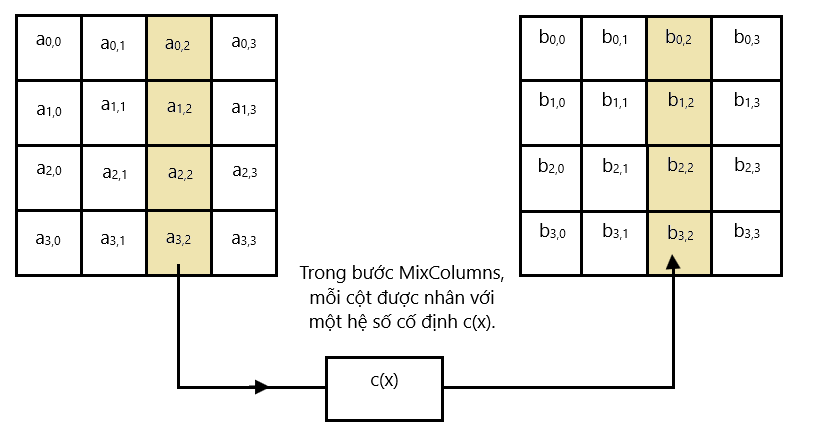
• Thực hiện mã hóa: Quá trình mã hóa gồm có nhiều vòng lặp (round), tùy vào độ dài của khóa ban đầu. Mỗi vòng lặp gồm có bốn giai đoạn: thêm khóa (add round key), thay thế byte (sub bytes), xoay hàng (shift rows) và trộn cột (mix columns). Các giai đoạn này được lặp lại cho đến khi đến vòng lặp cuối cùng, khi đó chỉ thực hiện ba giai đoạn: thêm khóa, thay thế byte và xoay hàng. Sau khi hoàn thành quá trình mã hóa, ta thu được khối dữ liệu đã được mã hóa.

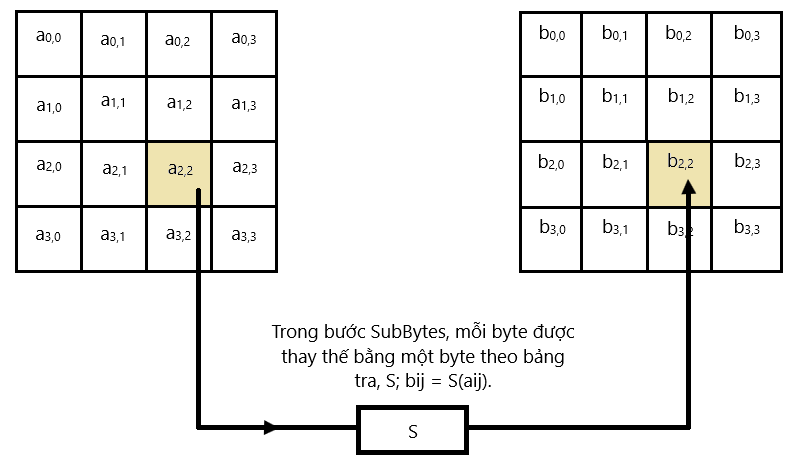
• • Cách tạo Rijndael S-box

Bảng S-box thuận được sinh ra bằng việc xác định nghịch đảo cho một giá trị nhất định trên GF(2^8) = GF(2) [x]/(x^8 + x^4 + x^3 + x + 1) (trường hữu hạn Rijindael). Giá trị 0 không có nghịch đảo thì được ánh xạ với 0. Những nghịch đảo được chuyển đổi thông qua phép biến đổi affine, công thức của phép biến đổi như sau:

Đầu vào của phép biến đổi là x và đầu ra là y, với mỗi giá trị x(0<=x <=255) thì ta sẽ nhận được một giá trị y tương ứng. Dưới đây là bảng S-box được sinh ra từ công thức trên.

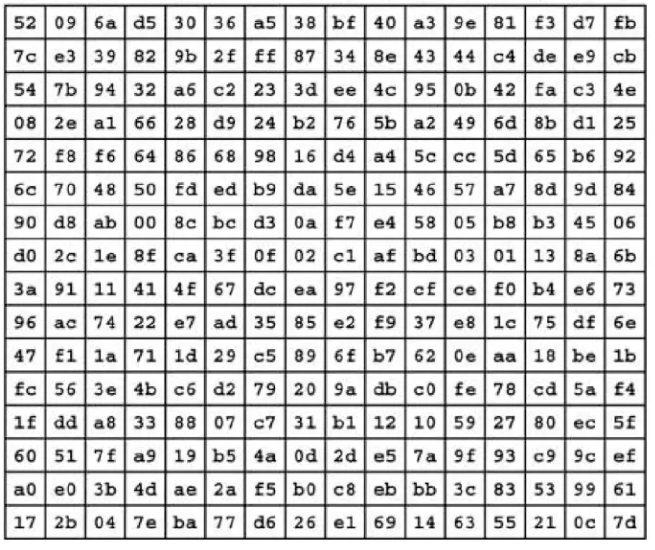
• Lặp lại cho các khối tiếp theo: Nếu dữ liệu gốc có nhiều hơn một khối, ta lặp lại các bước trên cho từng khối, sử dụng cùng một khóa bí mật. Có thể sử dụng các chế độ hoạt động (mode of operation) khác nhau để tăng độ bảo mật và ngẫu nhiên hóa của quá trình mã hóa, ví dụ như ECB (Electronic Code Book), CBC (Cipher Block Chaining), CTR (Counter), GCM (Galois Counter Mode)…

Chế độ	Mô tả	Ứng dụng
Electronic Codebook (ECB)	Dữ liệu đầu vào của thuật toán được XOR với khối mã hóa trước đó của bản mã để tạo ra khối bản rõ tiếp theo.	Truyền dữ liệu an toàn cho các giá trị đơn lẻ (ví dụ: khóa mã hóa)
Cipher Block Chaining (CBC)	Trong chế độ mã sách điện tử (ECB), mỗi khối dữ liệu của bản rõ được mã hóa độc lập với cùng một khóa.	Truyền dữ liệu dạng khối cho mục đích chung; Xác thực
Counter (CTR)	Một bộ đếm được mã hóa (CTR) được XOR với mỗi khối dữ liệu bản rõ, với bộ đếm được tăng dần cho mỗi khối tiếp theo.	Truyền dữ liệu an toàn cho các giá trị đơn lẻ (ví dụ: khóa mã hóa)
Galois Counter Mode (GCM))	Một chế độ dựa trên CTR, cung cấp mã hóa đồng thời và xác thực tích hợp bằng cách sử dụng Galois field để tạo mã xác thực.	Truyền dữ liệu tốc độ cao với xác thực tích hợp; Bảo mật mạng (ví dụ: TLS, IPsec)

3. So sánh RSA và AES

Đặc điểm	RSA (Bất đối xứng)	AES (Đối xứng)
Loại mã hóa	Sử dụng cặp khóa công khai-riêng	Sử dụng một khóa chung
Độ dài khóa	2048, 3072, 4096 bit	128, 192, 256 bit
Tốc độ	Chậm, chi phí tính toán cao	Nhanh, hiệu quả với dữ liệu lớn
Ứng dụng chính	Chữ ký số, SSL/TLS	Lưu trữ dữ liệu, bảo mật VPN
Ưu điểm	Bảo mật cao cho mã hóa công khai và chữ ký số.	Nhanh và hiệu quả với lượng dữ liệu lớn.
	Phù hợp với trao đổi khóa an toàn.	Yêu cầu ít tài nguyên tính toán.
Nhược điểm	Chậm, tốn nhiều tài nguyên.	Dễ gặp vấn đề nếu quản lý khóa không tốt.
	Không phù hợp để mã hóa dữ liệu lớn.	Khóa dùng chung phải được bảo vệ chặt chẽ.

4. Tóm lại

Trên đây là những thông tin liên quan đến thuật toán mã hoá bất đối xứng RSA và thuật toán mã hóa đối xứng AES. Hy vọng với những chia sẻ trên đây bạn đã nắm được đặc điểm, ứng dụng cũng như ưu điểm và hạn chế của RSA và AES.